El numero PHI - La divina proporcion.

                                                El Numero PHI

Phi, el número de oro. Matemáticamente hablando, podemos definirlo como aquel número al que, tanto si le sumamos uno como si lo elevamos al cuadrado, sale el mismo resultado.

Se trata de un número algebraico irracional (decimal infinito no periódico) que posee muchas propiedades interesantes y que fue descubierto en la antigüedad, no como “unidad” sino como relación o proporción entre segmentos de rectas. Esta proporción se encuentra tanto en algunas figuras geométricas como en la naturaleza. Puede hallarse en elementos geométricos, en las nervaduras de las hojas de algunos árboles, en el grosor de las ramas, en el caparazón de un caracol, en los flósculos de los girasoles, etc.

Asimismo, se atribuye un carácter estético a los objetos cuyas medidas guardan la proporción áurea. Algunos incluso creen que posee una importancia mística. A lo largo de la historia, se ha atribuido su inclusión en el diseño de diversas obras de arquitectura y otras artes, aunque algunos de estos casos han sido cuestionados por los estudiosos de las matemáticas y el arte.

Pirámide de Keops y torre Eiffel 

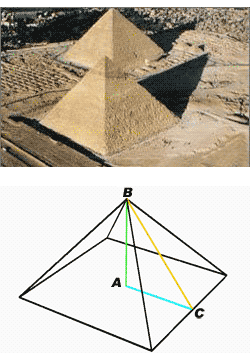Desde el antiguo Egipto se utiliza el numero Phi en la arquitectura. Por   ejemplo en la pirámide de Keops. Si la distancia AC es igual a 1, AB mide la raíz cuadrada de phi y BC mide phi.

  La pirámide de Keops mide 230 metros de lado, la base de la pirámide es cuadrada.

  AC = 230/2 = 115

  √Φ ≈ 1.272

  AB = √Φ --> √Φ x 115 ≈ 146,28 que son los metros de altura de la pirámide de Keops.

  BC = Φ x 115 ≈ 186,07 metros desde el centro de un lado de la base hasta el   pico de la pirámide. 

 

  La torre Eiffel guarda las proporciones de Phi.

      

Los ejes de sus cuatro pilares forman un cuadrado de 100 metros, que seria el lado pequeño de un rectángulo áureo. Pues poniendo dos rectángulos conseguimos la altura de esta torre.

100 x Φ x 2 ≈ 323,61 metros que es la altura de la torre. 

También se encuentra en las diferentes partes de la torre, vea el dibujo donde el espacio azul seria igual a uno y Phi seria el espacio azul más el dorado. 

La relación entre el techo y las columnas del Partenón, en Atenas (s. V a. C.). 

La relación entre las partes, el techo y las columnas del Partenón, en Atenas (s. V a. C.).Durante el primer cuarto del siglo XX, Jay Hambidge, de la Universidad de Yale, se inspiró en un pasaje del Theeteto de Platón para estudiar las proporciones relativas de las superficies, algo muy natural cuando se trata de obras arquitectónicas. Dos rectángulos no semejantes se distinguen entre sí por el cociente de su lado mayor por el menor, número que basta para caracterizar a estas figuras y que denominó módulo del rectángulo. Un cuadrado tiene módulo 1 y el doble cuadrado módulo 2. Aquellos rectángulos cuyos módulos son números enteros o racionales fueron denominados "estáticos" y los que poseen módulos irracionales euclidianos, o sea, expresables algebraicamente como raíces de ecuaciones cuadráticas o reducibles a ellas, "dinámicos". El doble cuadrado es a la vez estático y dinámico, pues 2 es la raíz cuadrada de 4. Posteriormente Hambidge estudió a los monumentos y templos griegos. Por medio de cuatro diagonales suministra las principales proporciones verticales y horizontales. Como dato adicional para indicar la complejidad del tratamiento del edificio se tiene que en 1837 fueron descubiertas correcciones ópticas en el Partenón. El templo tiene tres vistas principales y si sus columnas estuvieran efectivamente a plomo, todas sus líneas fuesen paralelas y perfectamente rectas y los ángulos rectos fueran exactos, por las propiedades de la visión humana el conjunto se vería más ancho arriba que en la base, sus columnas se percibirían inclinadas hacia afuera y la línea que fundamenta el techo sobre las columnas se vería como una especie de catenaria, con los extremos del edificio aparentemente más altos que el centro. Los constructores hicieron la construcción compensando estos efectos de ilusión óptica inclinando o curvando en sentido inverso a los elementos involucrados. Así las columnas exteriores,en ambos lados del frente, están inclinadas hacia adentro en un ángulo de 2,65 segundos de arco, mientras que las que están en el medio tienen una inclinación de 2,61 segundos de arco. La línea que formarían los dinteles entre columnas y que constituye la base del triángulo que corona el edificio, en realidad es un ángulo de 2,64 segundos de arco con el vértice más elevado que los extremos. De esta forma, y con otras correcciones que no se mencionan aquí, se logra que cualquier observador que se sitúe en los tres puntos principales de vista vea todo el conjunto paralelo, uniforme y recto.

                      
                           El numero PHI en el sistema solar.

En la tercera columna de la siguiente tabla el resultado es el de dividir la distancia del planeta al sol por la distancia del anterior, por ejemplo en Tierra dividimos 149,6 por 108,2 = 1,383 .

Para Mercurio, al no tener planeta anterior le hemos asignado 1.

Muchas veces cuando hablamos del sistema solar omitimos el cinturón de asteroides, también representa una masa considerable en el "equilibrio del sistema solar", siendo Ceres el asteroide mayor. Ceres es tan grande que tiene una forma esférica (como los otros planetas) y representa un tercio del total de la masa del cinturón de asteroides situado entre Marte y Júpiter. 

Planetas	Distancia al sol en millones de Km.	Relación entre las distancias de los sucesivos planetas
Mercurio	57,9	1
Venus	108,2	1,869
Tierra	149,6	1,383
Marte	227.9	1,523
Ceres	413,7	1,815
Júpiter	778,6	1,881
Saturno	1433,5	1,841
Urano	2872,5	2,004
Neptuno	4495,1	1,565
Plutón	5870	1,306

Total	16,187
Media	1,6187
Numero Phi	1,6180

                                             El numero PHI en el arte

Leda Atómica

El cuadro de Dalí Leda atómica, pintado en 1949, sintetiza siglos de tradición matemática y simbólica, especialmente pitagórica. Se trata de una filigrana basada en la proporción áurea, pero elaborada de tal forma que no es evidente para el espectador. En el boceto de 1947 se advierte la meticulosidad del análisis geométrico realizado por Dalí basado en el pentagrama místico pitagórico.

                                                                                                                    

El rosotro de la Gioconda, pintada por Leonardo, se encuadra en un rectángulo áureo.
Unas proporciones armoniosas para el cuerpo, que estudiaron antes los griegos y romanos, las plasmó en este dibujo Leonardo da Vinci. Sirvió para ilustrar el libro La Divina Proporción  de Luca Pacioli editado en 1509.
                                       
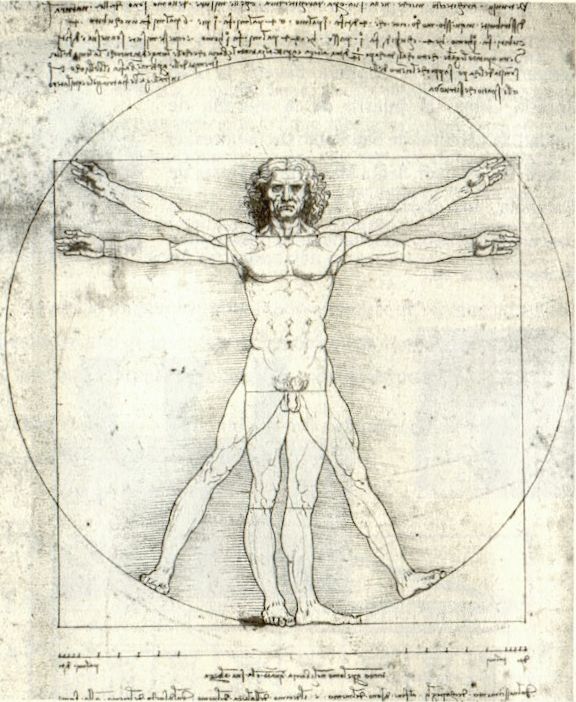
En dicho libro se describen cuales han de ser las proporciones de las construcciones artísticas. En particular, Pacioli propone un hombre perfecto en el que las relaciones entre las distintas partes de su cuerpo sean proporciones áureas. Estirando manos y pies y haciendo centro en el ombligo se dibuja la circunferencia. El cuadrado tiene por lado la altura del cuerpo que coincide, en un cuerpo armonioso, con la longitud entre los extremos de los dedos de ambas manos cuando los brazos están extendidos y formando un ángulo de 90º con el tronco. Resulta que el cociente entre la altura del hombre (lado del cuadrado) y la distancia del ombligo a la punta de la mano (radio de la circunferencia) es el número áureo.

                                 El numero aureo en la musica

Es necesario aclarar que cuando se menciona al número áureo en una realización artística de cualquier naturaleza no se está haciendo mención al número áureo de los matemáticos, un irracional con infinitos decimales, sino a una aproximación racional adecuada a las circunstancias o a un dibujo hecho con regla no graduada de un solo borde y longitud indefinida y un compás de abertura fija o variable. Generalmente se utilizan cocientes de números pertenecientes a la sucesión de Fibonacci que dan valores aproximados, alternativamente por defecto o por exceso, según la necesidad o la sensibilidad humana y hasta la capacidad de separación tonal de cada instrumento. Un violín, por ejemplo, puede separar hasta un tercio de tono. El oído humano sano y entrenado distingue hasta trescientos sonidos por octava. Como un ejemplo conocido y no discutido tenemos a la escala atemperada o templada. Esta es una escala logarítmica. Se creó muy poco tiempo después de que los logaritmos pasaran al patrimonio de la matemática. La octava atemperada está basada en la raíz duodécima de 2. Este número irracional tiene infinitos decimales, pero la afinación se hace redondeando las cifras de las frecuencias a uno o dos decimales. De cualquier manera, el error tonal total cometido no es superior al doceavo de tono y el oído humano no lo nota. La uniformidad de la separación de las notas y la coincidencia de bemoles y sostenidos permite comenzar una melodía por cualquier nota sin que se produzcan las desagradables disonancias de la escala diatónica y la escala física. De la misma manera se actúa con la distribución de tiempos o la altura de los tonos usando el número áureo; con una aproximación racional que resulte práctica. Existen numerosos estudios al respecto, principalmente de la Universidad de Cambridge.

    - Autores como Bártok, Messiaen y Stockhausen, entre otros, compusieron obras cuyas unidades formales se relacionan (a propósito) con la sección áurea.

    - El compositor mexicano Silvestre Revueltas (1899-1945) utilizó también el número áureo en su obra Alcancías, para organizar las partes (unidades formales).

    - El grupo de rock progresivo norteamericano Tool, en su disco Lateralus (2001) hacen múltiples referencias al número áureo y a la secuencia Fibonacci, sobre todo en la canción que da nombre al disco, pues los versos de la misma están cantados de forma que el número de sílabas pronunciadas en cada uno van componiendo dicha secuencia. Además la voz entra en el minuto 1:37, que pasado al sistema decimal coincide muy aproximadamente con el número áureo.

    - Zeysing notó la presencia de los números 3, 5, 8 y 13, de la Sucesión de Fibonacci, en el cálculo de los intervalos aferentes a los dos tipos de acordes perfectos. Los dos tonos del acorde mayor final, mi y do por ejemplo (la sexta menor o tercia mayor invertida en do mayor), están entre sí en la razón cinco octavos. Los dos tonos del acorde menor final, por ejemplo, mi bemol y do (sexta mayor o tercia transpuesta en do menor) dan la razón tres quintos.

http://es.wikipedia.org/wiki/N%C3%BAmero_%C3%

http://www.genciencia.com/2008/06/19-la-sucesion-de-fibonacci